CVAE
VAE回顾
VAE的目标是最大化对数似然函数
其中,
$\mathcal{L}(\theta, \phi; \text{x}^{(i)}) = \mathbb{E}{q{\phi}(\text{z}|\text{x})} [\log p_{\theta}(\text{x,z}) - \log q_{\phi}(\text{z}|\text{x})]= -KL(q_{\phi}(\text{z}|\text{x}^{(i)})||p_{\theta}(\text{z})) + \mathbb{E}{q{\phi}(\text{z}|\text{x}^{(i)})} \log p_{\theta}(\text{x}^{(i)}|\text{z})$
由于KL散度非负,对数似然函数的变分下界即为上式中的)项。一般来说,
)是未知的,或者难以获得显式表达式的,因此,直接优化对数似然函数是不可行的,一般转而优化它的变分下界,即上式中的
项。Diederik P.Kingma和Max Welling提出了两个算法SGVB和AEVB去估计
。
CVAE
VAE用的训练集是数据)。当生成数据时,由隐变量
)控制生成数据
),如果我们现在有的数据不只是
),我们还有关于数据
)的一些额外信息
,最简单的,以手写数字为例,它的标签0-9,那么我们是否能够利用上这些额外的信息呢?
CVAE-1
一个简答的想法,考虑条件概率分布,套用原来的VAE模型,我们不难作出以下推导:
$KL(q_{\phi}(\text{z}|\text{x,y})||p_{\theta}(\text{z}|\text{x,y})) = \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} \log \frac{q_{\phi}(\text{z}|\text{x,y})}{p_{\theta}(\text{z}|\text{x,y})} \
= \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} \log \frac{q_{\phi}(\text{z}|\text{x,y}) p_{\theta}(\text{x}|\text{y})}{p_{\theta}(\text{z}|\text{x,y}) p_{\theta}(\text{x}|\text{y})} \
= \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} \log \frac{q_{\phi}(\text{z}|\text{x,y}) p_{\theta}(\text{x}|\text{y})}{p_{\theta}(\text{x,z}|\text{y})} \
= KL(q_{\phi}(\text{z}|\text{x,y}) || p_{\theta}(\text{x,z}|\text{y})) + \log p_{\theta}(\text{x}|\text{y}))$
于是
其中,
$\mathcal{L}(\theta,\phi;\text{x,y}) = -KL(q_{\phi}(\text{z}|\text{x,y}) || p_{\theta}(\text{x,z}|\text{y})) \
= \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} [\log p_{\theta}(\text{x,z}|\text{y}) - \log q_{\phi}(\text{z}|\text{x,y})] \
= -KL(q_{\phi}(\text{z}|\text{x,y})||p_{\theta}(\text{z}|\text{y})) + \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} \log p_{\theta}(\text{x}|\text{y,z})$
类似于VAE,套用SGVB算法,再做一下reparameterization,取适当的分布和网络,我们就得到了一个CVAE模型。
我们姑且称这个版本的CVAE为CVAE-1模型,没错,CVAE模型不止一个……
CVAE-2
此外,与CGAN一样,我们一般假设额外信息)与隐变量
)没有直接的关系,因此条件概率
,于是变分下界可以写成
这在文献[3]中提到过。姑且称这个版本为CVAE-2模型。
CVAE-3
这就完了吗?文献[2]会告诉你,不要着急,我们也提出了一种CVAE。文中提出的方法不是产生数据),而是直接考虑预测问题:预测数据
)的标签
)。什么意思呢?它的似然函数是
)而不是
)。而这个推导也不难,事实上,把
)看成我们要生成的“数据”,
)看成是“标签”,在上面推导的结果里面直接交换
的位置,就得到了
其中,
$\mathcal{L}(\theta,\phi;\text{x,y}) = -KL(q_{\phi}(\text{z}|\text{x,y}) || p_{\theta}(\text{y,z}|\text{x})) \
= \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} [\log p_{\theta}(\text{y,z}|\text{x}) - \log q_{\phi}(\text{z}|\text{x,y})] \
= -KL(q_{\phi}(\text{z}|\text{x,y})||p_{\theta}(\text{z}|\text{x})) + \mathbb{E}{q{\phi}(\text{z}|\text{x,y})} \log p_{\theta}(\text{y}|\text{x,z})$
同样地,对)做一下reparameterization,写成
)。再取适当的分布和网络,就可以了。值得一提的是,我们会在模型中设定适当的分布
),当训练完了以后,可以把模型当成一个分类器,预测输入
的标签:
上面的预测涉及到求期望,除非有显式结果,否则一般采用均值去近似期望:
姑且这个模型称为CVAE-3,它的图模型结构如下:
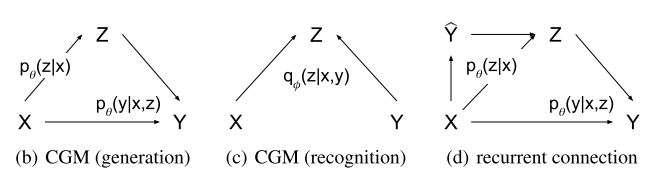
CVAE-4
非常抱歉地告诉你,CVAE模型还没完。文献[3]提出了CMMA模型(conditional multimodal autoencoder),实际上它也可以看成是条件版本的VAE。一般来说,我们考虑的CVAE或者CGAN的图模型是长这样的:
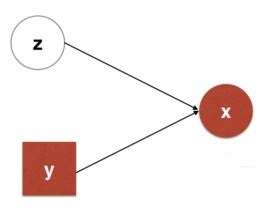
它的特点是一般是相互独立的。而CMMA考虑的图模型是长这样的:
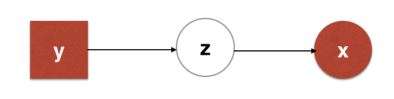
这个模型的特点是隐变量是由额外信息)确定的,
)。整个推导过程跟CVAE-1一模一样,应用
以后,变分下界可以简化为:
姑且称CMMA模型为CVAE-4。CVAE-4模型将标签信息编码到隐变量中,作者指出,这样做的效果更好。
当然,针对具体的问题,还有一些不一样的CVAE设计,例如,文献[1]用CVAE做半监督学习,用到的CVAE又与上面介绍的有所不同。根据具体问题,有些模型还会对目标函数添加一些惩罚项。
VAE是个贝叶斯模型,它的条件概率版本根据取条件概率的形式的不同,自然会出现多种多样的模型。
代码
\1. RuiShu/cvae: Conditional variational autoencoder implementation in Torch
\2. kastnerkyle/SciPy2015: Talk for SciPy2015 “Deep Learning: Tips From The Road”
\3. Tutorial on Variational Autoencoders
\5. jramapuram/CVAE: Convolutional Variational Autoencoder
参考文献
\1. Kingma D P, Mohamed S, Rezende D J, et al. Semi-supervised learning with deep generative models[C]//Advances in Neural Information Processing Systems. 2014: 3581-3589.
\2. Sohn K, Lee H, Yan X. Learning structured output representation using deep conditional generative models[C]//Advances in Neural Information Processing Systems. 2015: 3483-3491.
\3. Pandey G, Dukkipati A. Variational methods for conditional multimodal learning: Generating human faces from attributes. arXiv preprint[J]. arXiv, 2016, 1603.
\4. Walker J, Doersch C, Gupta A, et al. An uncertain future: Forecasting from static images using variational autoencoders[C]//European Conference on Computer Vision. Springer International Publishing, 2016: 835-851.
\5. Doersch C. Tutorial on variational autoencoders[J]. arXiv preprint arXiv:1606.05908, 2016.